Калькулятор позволяет онлайн найти площадь треугольника прямоугольного, равнобедренного, равностороннего и разностороннего различными способами.

Калькулятор позволяет онлайн найти площадь треугольника разностороннего , треугольника прямоугольного , треугольника равнобедренного , треугольника равностороннего различными способами и выводит формулы с подробным решением.

• 1. Разносторонний треугольник:
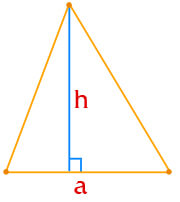
• 1.1. по основанию и высоте: площадь треугольника равна произведению половины основания на его высоту;
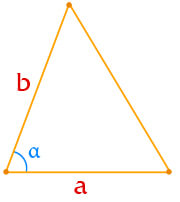
• 1.2. по двум сторонам и углу между ними: площадь треугольника равна половине произведения его сторон на синус угла между ними;
• 1.3. по четырем сторонам (формула Герона): площадь треугольника равна корню из произведения разностей полупериметра треугольника и каждой из его сторон;
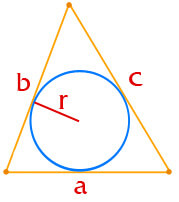
• 1.4. по радиусу вписанной окружности и трем сторонам: площадь треугольника равна произведению полупериметра на радиус вписанной окружности;
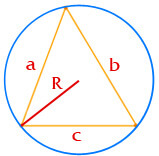
• 1.5. по радиусу описанной окружности и трем сторонам: площадь треугольника равна одной четвертой отношения произведения сторон на радиус описанной окружности.

• 2. Прямоугольный треугольник:
• 2.1. по основанию и высоте: площадь прямоугольно треугольника равна половине произведения катетов треугольника;
• 2.2. по отрезкам на которые делит гипотенузу вписанная окружность: площадь прямоугольно треугольника равна произведению произведению отрезков на которые делит гипотенузу вписанная окружность;
• 2.3. по четырем сторонам (формула Герона): площадь прямоугольно треугольника равна произведению разностей полупериметра треугольника и каждой его катетов.

• 3. Равнобедренный треугольник:
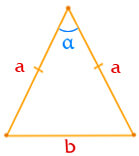
• 3.1. по боковым сторонам и углу между ними: площадь равнобедренного треугольника равна половине произведения квадрата боковой стороны на синус угла между боковыми сторонами;
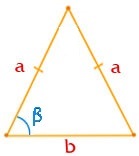
• 3.2. по боковой стороне, основанию и углу между боковыми сторонами и основанием: площадь равнобедренного треугольника равна половине произведения боковой стороны и основания на синус угла между ними;
• 3.3. по основанию и углу между боковыми сторонами и основанием: площадь равнобедренного треугольника равна четверти отношения квадрата основания на тангенс половинного угла между боковыми сторонами.

• 4. Равносторонний треугольник:
• 4.1. по стороне: площадь равностороннего треугольника равна произведению одной четвертой корня из трех на квадрат стороны;
• 4.2. по радиусу описанной окружности: площадь равностороннего треугольника равна произведению трех четвертей корня из трех на квадрат радиуса описанной окружности;
• 4.3. по радиусу вписанной окружности: площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.
• 4.4. по высоте: площадь равностороннего треугольника равна отношению квадрата высоты к корню из трех.

Площадь треугольника по основанию и высоте

Площадь треугольника по двум сторонам и углу между ними

Площадь треугольника по формуле Герона

Площадь треугольника по радиусу вписанной окружности и трем сторонам

Площадь треугольника по радиусу описанной окружности и трем сторонам

Площадь прямоугольного треугольника по двум катетам

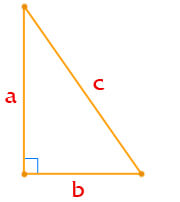
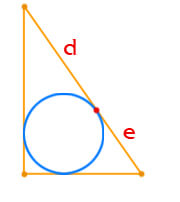
Площадь прямоугольного треугольника по отрезкам на которые делит гипотенузу вписанная окружность

Площадь прямоугольного треугольника по формуле Герона

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между боковыми сторонами и основанием

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами и основанием

Площадь равностороннего треугольника по стороне

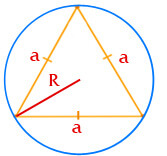
Площадь равностороннего треугольника по радиусу описанной окружности

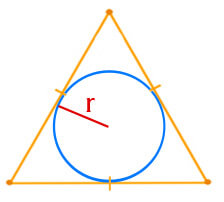
Площадь равностороннего треугольника по радиусу вписанной окружности

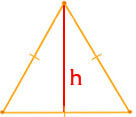
Площадь равностороннего треугольника по высоте

Помощь на развитие проекта premierdevelopment.ru

Send mail и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Для справки:

треугольник

— геометрическая фигура, образованная соединением отрезков трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки - его сторонами.

площадь геометрической фигуры

— численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

II. Примечание:

1. Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.