Онлайн калькулятор расчета площади поверхности правильной пирамиды с отображением формул и подробным решением.
Калькулятора онлайн рассчитывает площадь боковой и полной поверхности правильной треугольной пирамиды и выводит формулы с подробным решением:
- площадь боковой Sside правильной треугольной пирамиды сумме площадей ее боковых граней;
- площадь полной Sfull правильной треугольной пирамиды сумме площадей ее основания и трех боковых граней.
| Исходные данные: | Решение: | |||
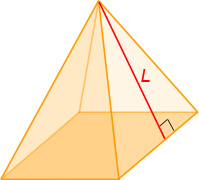
| Апофема (опущенный перпендикуляр из вершины на ребро основания) |
L = |
площадь боковой поверхности: расчет площади полной поверхности правильной треугольной пирамиды площадь полной поверхности: расчет площади боковой поверхности правильной треугольной пирамиды |
|
|
| Периметр основания | P = | |||
| Площадь основания | Sосн = | |||
I. Для справки:
1. Пирамида - это многогранник, у которого одна грань - основание пирамиды - произвольный многоугольник, а остальные - боковые грани - треугольники с общей вершиной, называемой вершиной пирамиды. Перпендикуляр опущенный из вершины пирамиды на ее основание, называется высотой пирамиды. Пирамида называется треугольной, четырехугольной, и т.д., если основанием пирамиды является треугольник, четырехугольник и т.д. Треугольная пирамида есть четырехгранник - тетраэдр. Четырехугольная - пятигранник и т.д.
2. Правильная пирамида - пирамида основание которой - правильный многоугольник, а высота опускается в центр основания. В правильной пирамиде все боковые ребра равны, все боковые грани равные равнобедренные треугольники.
3. Площадь геометрической фигуры - численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
4. Площадь поверхности - аддитивная числовая характеристика поверхности.